管理科学-上

发表于 更新于 分类于

  1. 有8口海上油井，相互间距离如下表所示（单位：海里）。其中1号井离海岸最短长度，为5海里，先要从海岸经1号井铺设油管将各井连接起来，则铺设输油管道的最短长度（）海里。

    • 9.1
    • 9.2
    • 10.1
    • 10.2

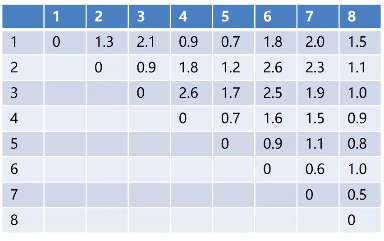
    image-20230830105824104

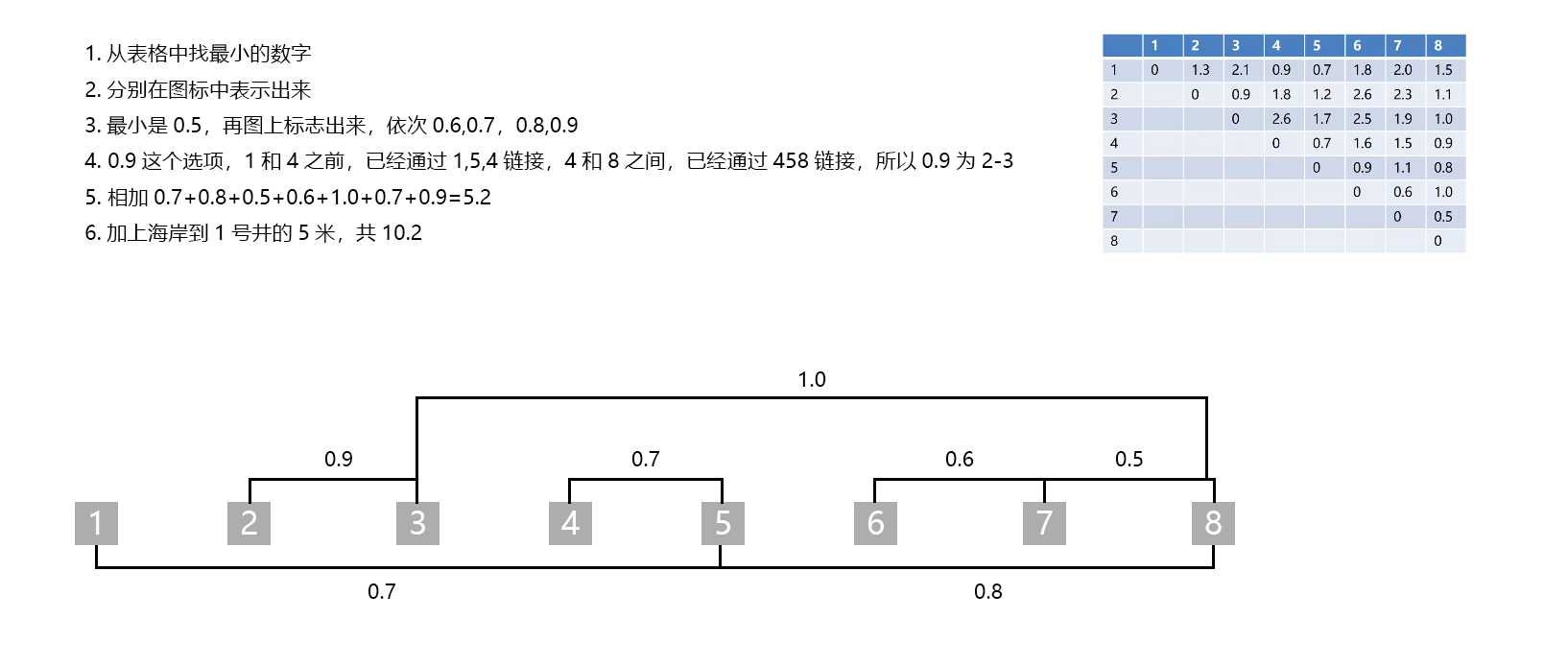
    最小生成树

    image-20230830154101750

  2. 如图所示，有一批货物要从城市S发送到T，线条上数字代表通过这条路的费用（单位为万元）。那么运送这批货物，至少需要花费多少元？81万元

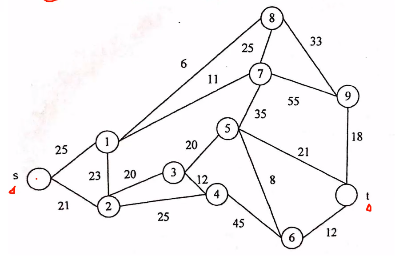
    image-20230830154527103

    最短路径

    1. 先算S到1的最小距离，
      1. 列举S到1的距离，S1==25;S21==41，
      2. 选最小25，写到1上
    2. 再算2,3一次得出，有多条的 先随便选一条

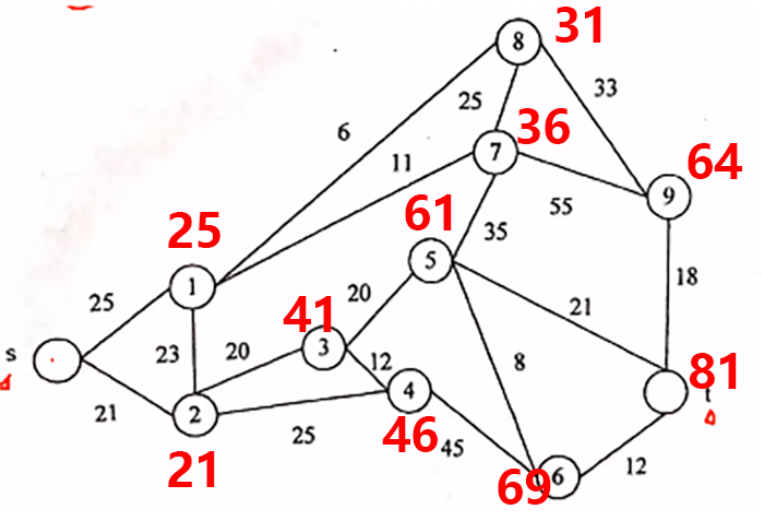
    image-20230830173546949

  3. 下图中标出了某地区的运输网，各节点之间的运输能力，那么，请节点1到节点6最大运输能力（流量）可以达到多少万吨/小时。

    • 23万吨

    image-20230830173900232

    解析：

    网络与最大流量

    • 列出1256，最大运输能力6，画图

      image-20230830174618294

    • 列出1356，最大运输能力10，画图

      image-20230830174703345

    • 列出156，最大运输能力5，画图

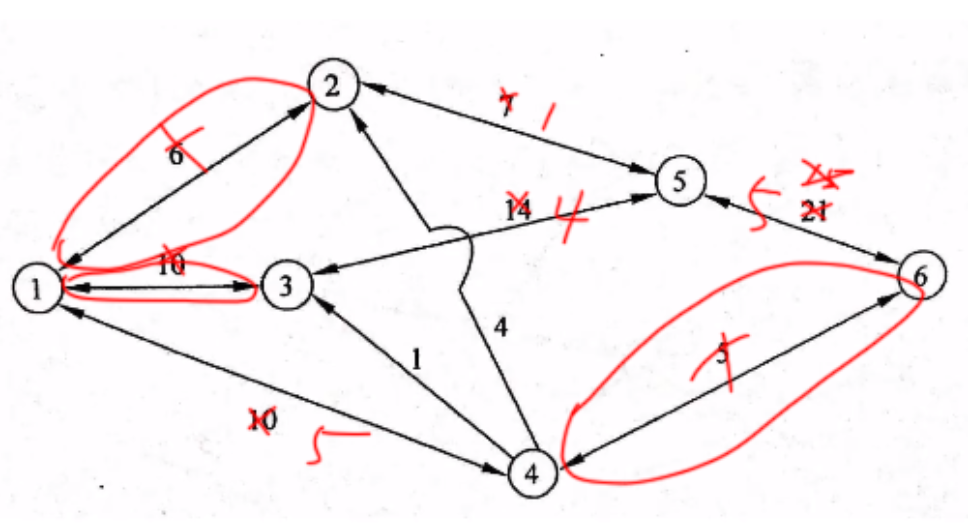
      image-20230830174847556

    • 列出14356，最大运输能力1，画图

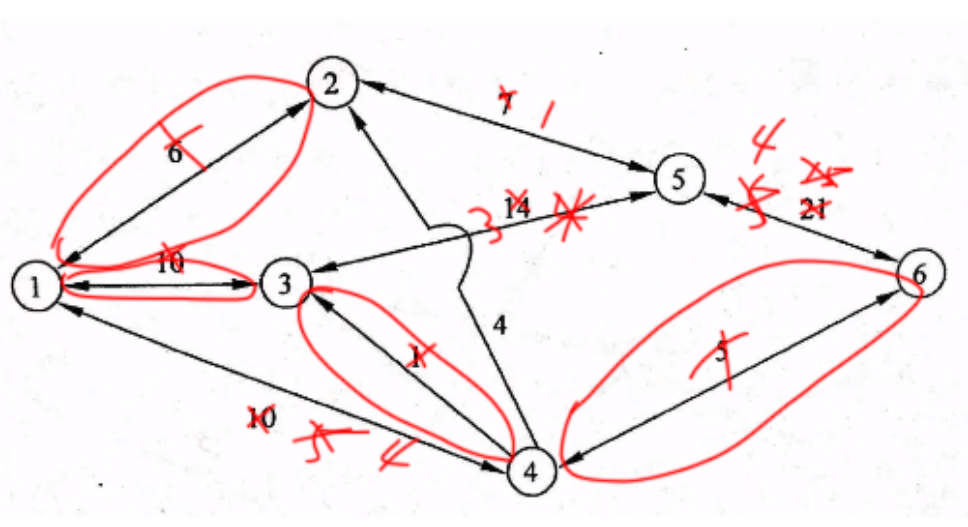
      image-20230830174936308

    • 列出14256，最大运输能力1，画图

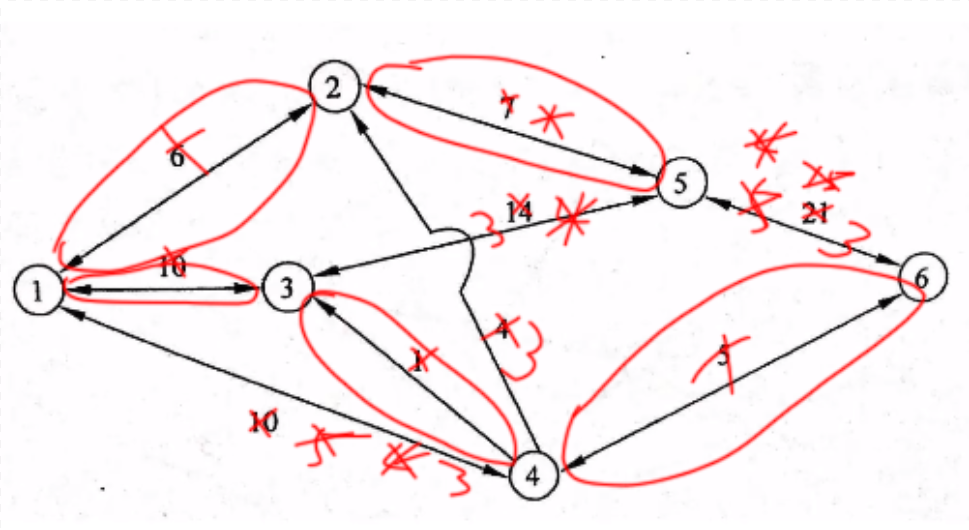
      image-20230830175032851

    • 无路可去，把之前的最大运输能力相加

      • 6+10+5+1+1=23

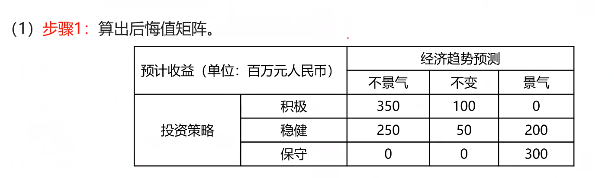
  4. 某公司需要根据下一年度宏观经济的增长趋势预测决定投资策略，宏观经济增长趋势有不景气，不变与景气三种，投资策略有积极、稳健和保守三种，各种状态的收益，如下图所示。

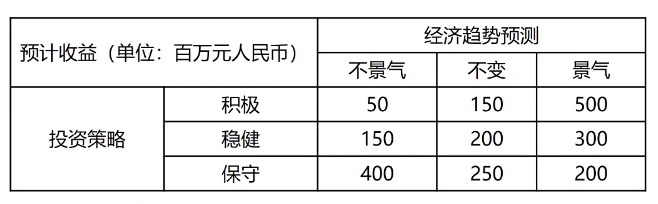
    image-20230830175528697

    【问题1】根据乐观主义准则的最佳决策是？

    500，所以选择积极。

    【问题2】根据悲观主义准则的最佳决策是？

    200，所以选择保守。

    【问题3】根据后悔值准则的最佳决策是？

    稳健方案。

    解析：

    不确定型决策

    image-20230831164428860

    因为考虑到收益，所以，取各自眼中最大的。

    image-20230831165256266

    image-20230831165541925

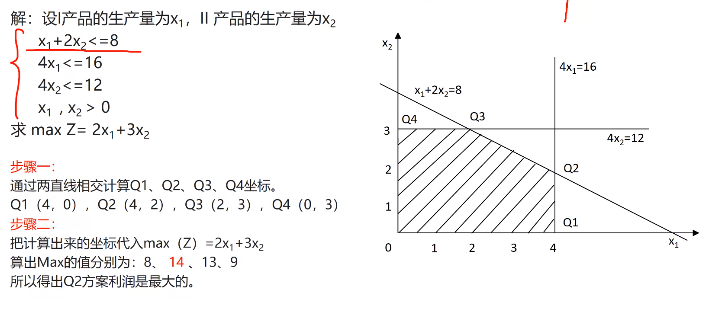
  5. 某工厂在计划期内要安排生产I，II两种产品，已知单位产品所需的设备台数及A、B两种原料消耗，如图所示：

    image-20230831165903516

    该工厂每生产意见I可获利2元，每生产一件产品II可获利3元，问应该如何安排计划使该工程获利最多。

    解析：

    image-20230831170830119

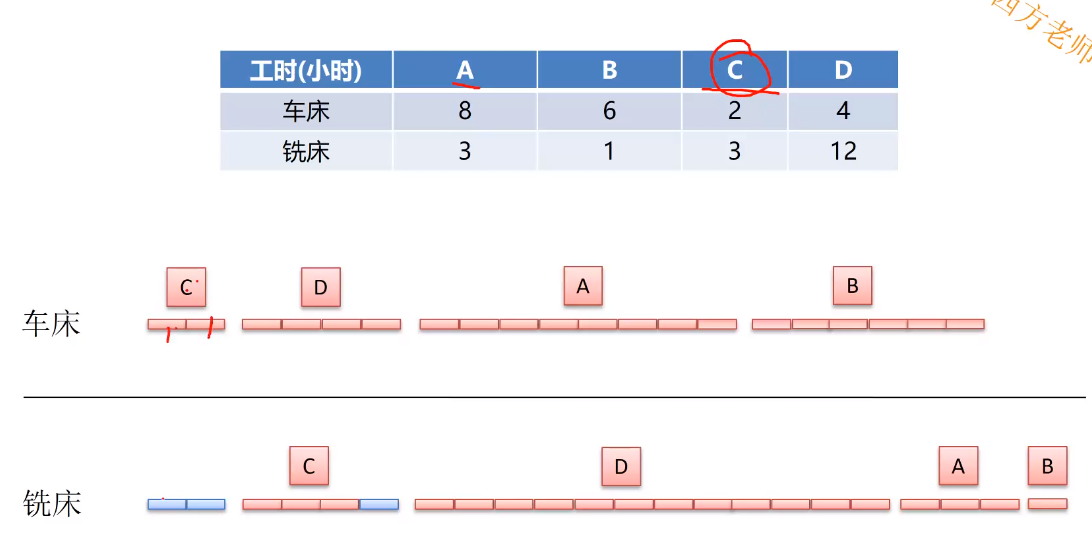
  6. 某车间需要一台车床铣车加工A、B、C、D四个零件。每个零件都需要先用车床加工，再用铣床加工。车床与铣床加工每个零件所需的工时（包括加工前的准备时间以及加工后的处理时间）如下表：image-20230831171736800

    若以A、B、C、D零件顺序安排加工，则共需32小时。适当调整零件加工顺序，可使所需总工时最短。在这种最短总工时方案中，零件A在车床上的加工顺序安排在第（1）位，四个零件加工共需（2）小时。

    第3位，22个小时。

    解析：

    image-20230831172604829

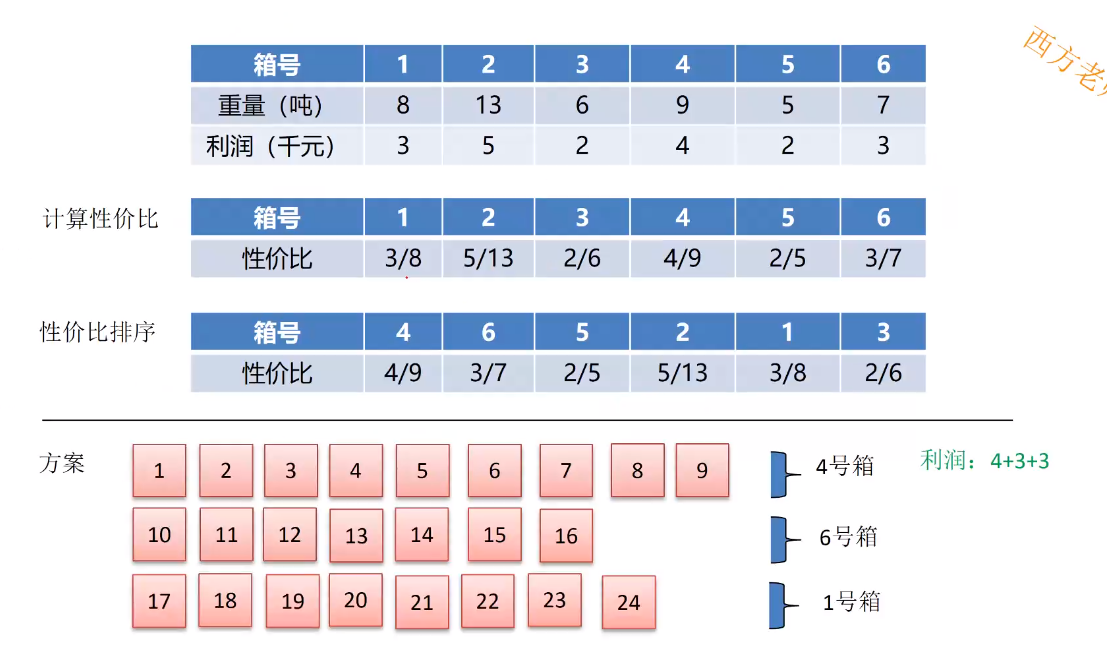
  7. 载重量限24吨的某货源飞机执行将一批金属原料运往某地的任务。待运输的各箱原料的重量、运输利润如下表所示。image-20230831172908977

    经优化安排，该飞机本次运输可以获得的最大利润为（）千元。

    • 11
    • 10
    • 9
    • 8

    解析：

    image-20230831173628425

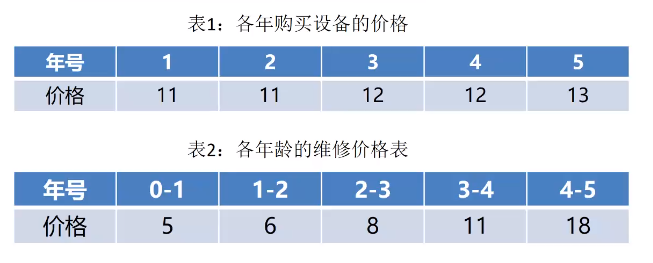
  8. 一家公司需要确定使用期为5年的一种设备的更换策略。已知各年购买设备的价格和各年龄设备的维修价格如表1和表2所示，最优的设备更换策略中，总费用是（）。image-20230902155545019

    • 50
    • 53
    • 59
    • 71

    解析：

    这个很简单假定1，2，3，4，5年换把费用加下就好。

    第1年购置，用到坏：

    11（购入设备）+5（第1年修）+6（第2年修）+8（第3年修）+11（第4年修）+18（第5年修）=59

    第1年购置，第2年换新的用到坏：

    11（购入设备）+5（第1年修）+11（购入设备）+5（第1年修）+6（第2年修）+8（第3年修）+11（第4年修）=57

    第1年购置，第3年换新的用到坏：

    11（购入设备）+5（第1年修）+6（第2年修）+12（购入设备）+5（第1年修）+6（第2年修）+8（第3年修）=53

    第1年购置，第4年换新的用到坏：

    11（购入设备）+5（第1年修）+6（第2年修）+8（第3年修）+12（购入设备）+5（第1年修）+6（第2年修）=53

    第1年购置，第5年换新的用到坏：

    11（购入设备）+5（第1年修）+6（第2年修）+8（第3年修）+13（第4年修）+11（购入设备）+5（第1年修）=59

  9. 某公司现有400万元用于投资甲乙丙三个项目，投资额以百万元为单位，已知由乙内三项投资的可能方案及相应获得的收益如下表所示：image-20230902161142660

    则该公司能获取的最大收益是（）百万元。

    • 17
    • 18
    • 20
    • 21

    解析：

    求最值问题

    也很简单，分三个情况，全投一个的最大产出，全投2个人，3个人都投

    全投1个人：选丙，得15

    全投2个人：有2个组合

    • 1+3组合，选甲丙4+11=15
    • 2+2组合，选乙丙9+8=17

    全投3个人：1+2+1，选甲乙丙4+9+5=18

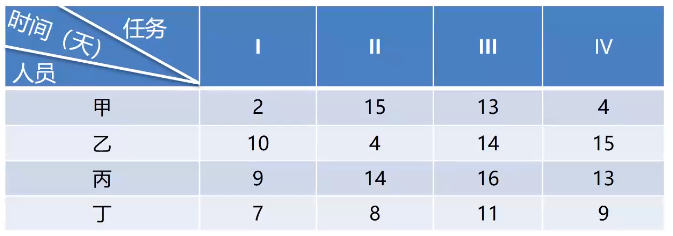
  10. 某项目有I、II、III、IV四项不同任务，恰有甲、乙、丙、下四个人去完成各项不同的任务，由于任务性质及每人的技术水平不同，他们完成各项任务所需时间也不同，具体如下表所示：image-20230902162142021

    • I
    • II
    • III
    • IV

    解析：

    匈利牙法

    image-20230902162933930

    减去同行最小的值，找出0值

    一眼确定，乙只能做II，甲I或IV，丙I，下I，II，IV都行

    甲，丁在III IV求最小值

    得2+4=6，故丁在III

    也可以把列上没有0的，也归0.得

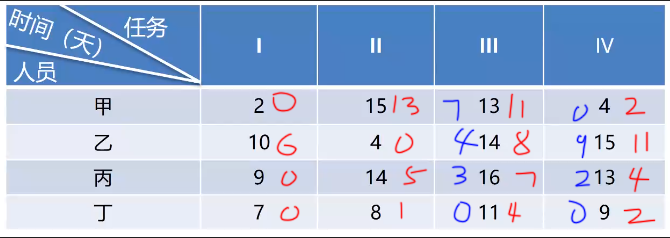
    image-20230902163408828

    选0的就好。

  11. 某航空公司为满虽客运量日益增长的需求，拟购置一批新的远程、中程及短程的喷气式客机。每架远程客机价格670万美元，中程客机500万美元，短程客机350万美元。该公司现有资金12000万美元用于购买飞机。据估计每架远程客机的年净利润为82万美元，中程客机的年净利润为60万美元，短程客机的年利润为40万美元。假设该公司现有的熟练驾驶员可支持30架新购入飞机的飞行任务，维修能力足以满虽新增加40架短程客机的维修要求，而每架中程客机维修量相当于4/3架短程客机，每架远程客机维修量相当于5/3架短程客机，为获取最大利润，该公司应购买各类客机分别为（）架。

    • 远程17，中程1，短程0
    • 远程15，中程1，短程2
    • 远程12，中程3，短程3
    • 远程10，中程3，短程3

    直接代入下答案会更快

    A：17x82+1x60=1454

    B：15x82+1x60+2x40=1370

    C：12x82+3x60+3x40=1284

    D：10x82+3x60+3x40=1120

    记得要看下是不是满足条件：

    1、不超过预算12000

    2、驾驶员不超过30

    3、维修费不超过40

  12. 某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点（销地）出售，各工厂的生产量（单位：吨）、各销售点的销售量（单位：吨）以及各销售点的单位运价（百元/吨）示于表所示：

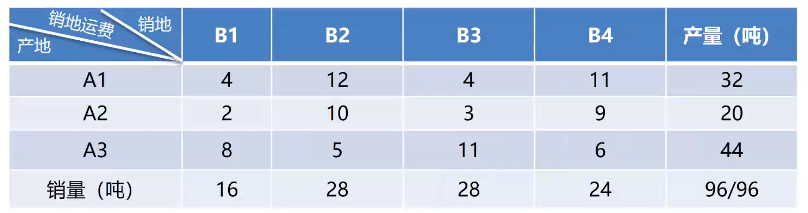
    适当安排调运方案，最小总运费为（）百元。image-20230902165628773

    • 450
    • 455
    • 460
    • 465

    解析：

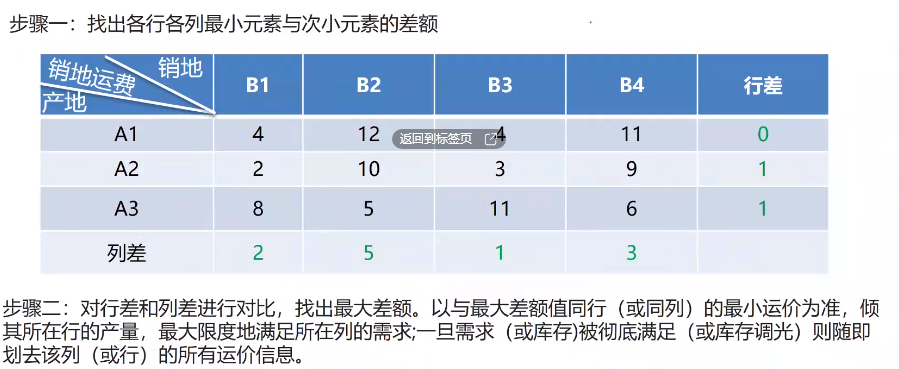
    伏格尔法image-20230902170914757

    所以，第一步：

    A3的最大化满足B2的销售，得到到运费为28x5=140，此时A3还有44-28=16

    再看B4，A3又是最小，把仅剩的16全部给B4，得16x6=96，但此时B4还有还有8个销售，用A2全部注入，得8x9=72，此时B4空了，B2也空了，且A2还有12，A1还有32

    再找B1，里面A2最小，A2梭哈12x2=24，B1销售还有16-12=4，A1，注入4，的4x4=16。

    此时，B1，B2,B3，B4销售没了，A1，只有32-4=28

    A1再B3销售，B3刚好28，等28x4=112

    加在一起：112+28+16+24+64+140=460